今日は波が高いとのこと。

昨日はSNSでは有義波高の画像が張られていた。

有義波高とは何か？というと「来た波の上位三分の一の平均をとったもの」ということらしい。

例えば、一時間に１ｍの波が６６回、３ｍの波が３３回来たら有義波高は１ｍの波を無視して３ｍの平均で割るので３ｍが有義波高。

波の高さが「レイリー分布」という確率分布というものに従うかららしい。

確率分布というのは何かというと確率みたいなもの。

サイコロはどの目が出る確率も同様なので「一様分布」という確率分布に従う。

波の高さは少々複雑なのでレイリー分布という確率分布に従う、ということらしい。


正規分布は自然界で一番よく出てくる確率分布。


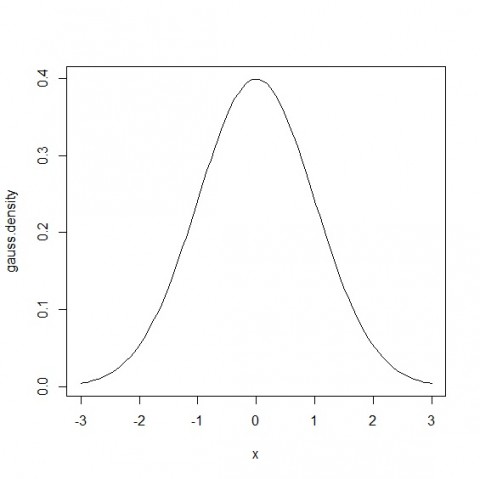
これが正規分布の図。真ん中の値が一番起きやすい、というグラフ。

人間はこれを感覚で知っていて、平均が一番起こりやすい、というのが分かっている。

ネットニュースで統計の錯覚みたいな話で、平均年収の話が出るけど、平均年収の分布が一様じゃないから平均で話してもしょうがない、とかは確率分布の話。

年収は「対数正規分布」というものに従っているらしい。

まぁ確率分布の言葉くらいは知ってないとデータを見ることはできないといっていいかもしれない。

 

昨日調べてみたら、
正規分布に従う確率変数X、Yの同時確率P(X=x,Y=y)がレイリー分布とのこと。

なんのこっちゃだけど、同時確率とは一緒に起きる確率という事。

正規分布の乱数を二つ用意してプロットしたその距離がレイリー分布、と書いてあったのでやってみました。

これは正規分布に従う乱数X,Yを１０００個用意しました。


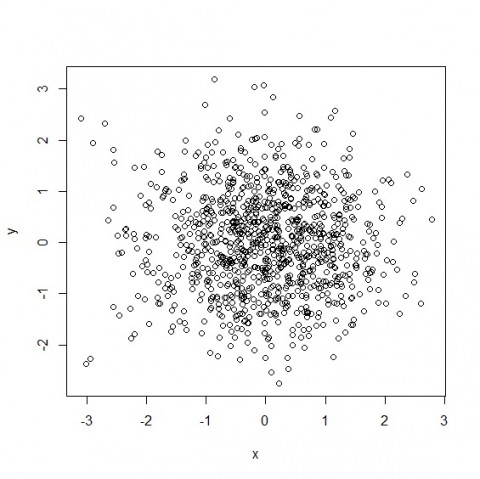
真ん中ほど色が濃いです。

なぜかというと、正規分布は真ん中が一番頻度が多いから。

X軸、Y軸で０を含みながら断面図を見ると正規分布のさっきのグラフになります。

次に距離のグラフを取ります。

なぜ距離なのかというとX,Yを同時に満たすのが原点からの距離だから。（そんなこと言ったら自由度１のχ二乗分布もレイリー分布じゃないかと思うけど統計の知識がなくて謎。）





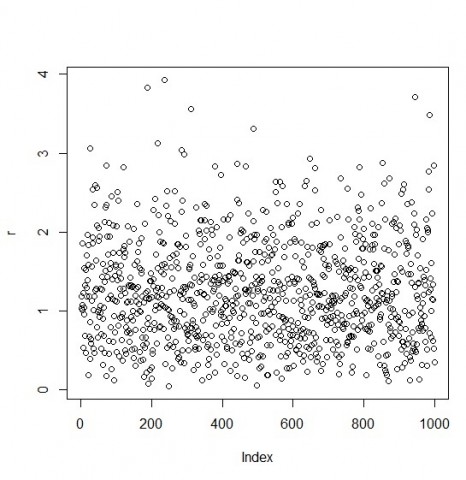
これがレイリー分布になるらしい。


レイリー分布のグラフも書いてみる。



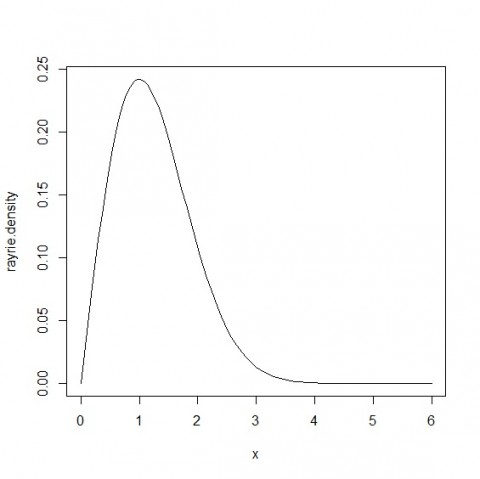
たしかに１が一番多いというグラフになっていそう。

４くらいの値になるとほぼ無い。

この多いところの波の平均を使わずに、要するに１の値の近くを使わずに、大きい方から順に数えるのは多分事故とかが起きないようにだろう。

例えば、このデータでいうと、もっとも出やすい値である最頻値が１ｍだとしても１０００波に１波くらいは４ｍくらいの波が来ているわけだ。

実際はこれは関数を規格化していないので４mの波が来ることはないだろうけど。

実際は有義波高１，５倍くらいまでが最大波であるらしい。

磯に上がったりするときよく見てから上がらないと不意に大波が来るというのはこういう、「レイリー分布に従う」という波の性質によるわけなのだ。