プロフィール

BlueTrain

茨城県

プロフィール詳細

カレンダー

<< 2026/2 >>

日 月 火 水 木 金 土
1 2 3 4 5 6 7
8 9 10 11 12 13 14
15 16 17 18 19 20 21
22 23 24 25 26 27 28

検索

:

アーカイブ

アクセスカウンター

  • 今日のアクセス：98
  • 昨日のアクセス：181
  • 総アクセス数：1399023

QRコード

▼ 釣りに超使える数学、ドモルガンの定理。

  • ジャンル:日記/一般
高校の数学で、ド・モルガンの定理というものを習う。

憶えていない人も居ると思うけど（Aの排反事象∪Bの排反事象）の排反事象はA∩Bになるという定理。


この定理、憶えるのが難しいのは（Aの排反事象∪Bの排反事象）の部分だろう。



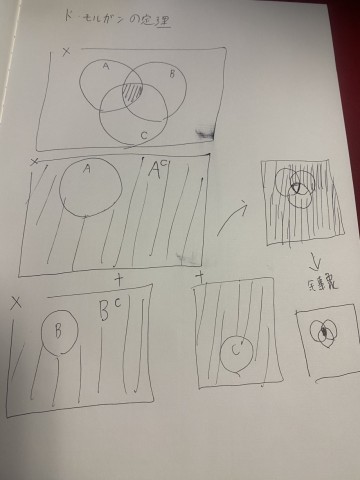
図で書くとこんな感じ。


AじゃないものとBじゃないものの全体を足し合わせてその余事象はAとBの共通という定理。

かなり憶えずらい。

しかし、ヒラメで考えると結構簡単に憶えられる。


ヒラメが釣れる状況、例えば澄潮で釣れる、とする。

これが事象Aに対応する。

次に、ヒラメが釣れる状況、朝まずめで釣れる、とする。

これが事象B。

これの排反事象を取るんだから、澄潮の排反は濁り、朝まずめの排反はそれ以外の時間帯。

それらの足しわせた状態、濁っていてか朝まずめの排反だから、濁っているか朝まずめでないときは釣れないのであれば、澄潮かつ朝まずめで釣れる、と同義になる。

これはかなり釣りに活かせる定理というのがお分かりだと思う。

釣れ無い状況を足し合わせるだけで、この状況なら釣れるというのが求まるのだ。



最近、測度論というのを趣味で勉強していて、カタクチをヒラメで測ることは可能かどうかを検討したりしている。

測度論というのは境界の話みたいで、ギリギリの際を数学で議論する。

こういう勉強はとにかくアウトプットするに限るのでこうやってブログに書いて勉強している次第です。

ご迷惑をお掛けしました。

コメントを見る