プロフィール

BlueTrain
茨城県
プロフィール詳細
カレンダー
検索
タグ
アーカイブ
アクセスカウンター
- 今日のアクセス:198
- 昨日のアクセス:237
- 総アクセス数:1402961
QRコード
▼ ルアー釣りを誤差から考えました。
- ジャンル:ニュース
ここのところ練習と称してヒラツイカップの為に地形の確認をしていました。
結構な数のポイントを作成したけど、まだまだ情報集め中。
昨日は久々の場所にIN。
着いてみると早速ヒラメを持ってる方がいらっしゃってその場所に入ってシーバスからのアタリが3回。

なんとか1キャッチできたけど竿の使い方を忘れてしまっていて一回バラシ。
大会前に確認できてよかったです。
自分は理系の大学に入ったのですが、その時に物理実験の先生が、
「計測というのは必ず誤差を含むから正確な値は分からない」
と仰っていました。
全く以て感覚的に分かりずらい話なのですが、例えば3cmの長さを測ったとしても、人間が測る以上、それには必ず誤差が含みます。
3cmを測ると±σという誤差が出てその範囲に真の値が含まれているという話です。
そうすると、人間が測るものというのは真の値+誤差になります。(なるはず)
これが世の中でまかり通っている、「3cmを測った」ということになります。
感のいい方ならもう言いたいことがお分かりかと思いますが、「ヒラメのベイトがイワシだけだといっても必ず誤差が付くからヒラメから他のベイトが出てきたとしてもそれは誤差で真の値はイワシだけだといいたいんじゃないのか?統計数学を悪用してポジショントークしようとしているだけじゃないか」と思われるかもしれませんがその通りです。
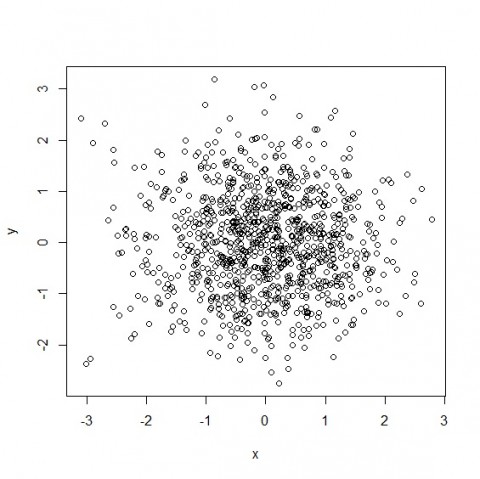
下の図の場合は真の値が「0」ですが、計測した値はバラバラです。
下の図はy=xが正しいモデル式
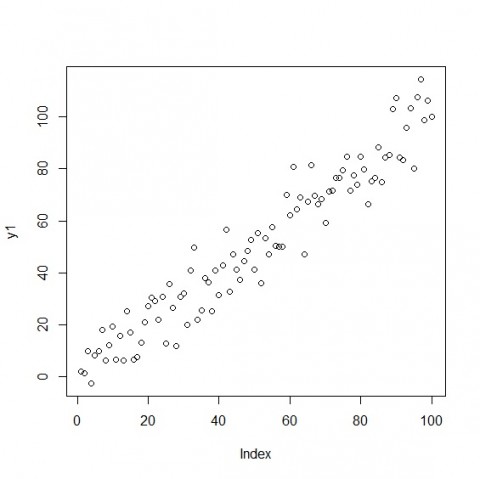
現実というのはたとえy=xが真実だとしてもy=x通りにはデータの値が出てくれないものなのです。多分。
もし「ヒラメのベイトがイワシだけ」というのが真実だとしても現実には「ヒラメの腹から出てくるのは イワシ+α(誤差)」でも問題はないと自分は思います。
相関関係で因果関係かどうかというような問題もあったりしますが、LiNGAMという新しい方法で因果と相関について勉強中です。
勉強は絶賛座礁中。
ベイトの話は僕のアンチの活性が上がってしまうのであんまりしないことにして、この誤差を考える時結構面白いなぁと思ったのが、
「ルアー釣りは魚の誤差」しか対象にしていないという事。
普通、世の中のものはなんでも「誤差を少なくする」ことに力を入れておりますが、ルアー釣りの場合は魚に餌じゃないものを食べさせる、という事をやろうとしているので、魚の習性+α(誤差)のα(誤差)だけでやる釣りです。
これがエサ釣りだと「魚の習性+α(誤差)」で釣りをするので現実的な釣りと言えます。
例えばヒラメにイワシの泳がせ釣りを使うのはイワシを追っているヒラメの本来の習性、それにもしかしたら糸に垂らされているイワシに対するなんらかの反応という誤差を含むので「現実=虚構+真実」ということになります(なると思います)。
youtubeで村岡さんの動画を観ていると「釣れるシーバスは数割」みたいなことを仰っていて、寧ろルアーでは釣れる方が誤差だと思います。
これはルアー釣りに大きなヒントになりそうな気がします。
例えば一つ仮定を立ててみる。
「魚が本来の習性が最大限の時(真の魚の習性からの誤差が小さい時)、ルアーでは釣れなくなる」
「一方、回遊から外れた魚、本来の海域にいない(誤差が大きくなっている時)魚はルアーへの反応がよくなる」
例えば、摂餌中の魚はルアーへの反応が鈍くなったりするけど、餌を食ってなくて何しているかちょっと分からないような魚は結構ルアーに反応がいい、というようなことが起きているのかもしれない。
この仮定が真なら、「ルアーで夜によく釣れる魚は昼行性」といえる。
「ルアーを噛むのは魚の習性を利用したもの」ではなく「魚の習性の誤差」という話だったのですが、反例(否定するような内容の例)となるような話では、弟の持っている本に「絶対口を使わない渓流魚に口を使わせるテンカラ釣りの漁師の秘伝の方法がある」との事。
洪水の時で魚が絶対に餌を食べない状態でも必ず釣って帰るという漁師さんがいらっしゃって、そういう方法があるみたい。
現実=誤差+真実なのに誤差の方がデカいのはおかしいからさっきの仮説が否定されてしまう。
結構飛躍した話になったけど、なんか面白そうなネタを得たので色々検証したいと思います。
結構な数のポイントを作成したけど、まだまだ情報集め中。
昨日は久々の場所にIN。
着いてみると早速ヒラメを持ってる方がいらっしゃってその場所に入ってシーバスからのアタリが3回。

なんとか1キャッチできたけど竿の使い方を忘れてしまっていて一回バラシ。
大会前に確認できてよかったです。
統計数学を使った釣りの考え
自分は理系の大学に入ったのですが、その時に物理実験の先生が、
「計測というのは必ず誤差を含むから正確な値は分からない」
と仰っていました。
全く以て感覚的に分かりずらい話なのですが、例えば3cmの長さを測ったとしても、人間が測る以上、それには必ず誤差が含みます。
3cmを測ると±σという誤差が出てその範囲に真の値が含まれているという話です。
そうすると、人間が測るものというのは真の値+誤差になります。(なるはず)
これが世の中でまかり通っている、「3cmを測った」ということになります。
感のいい方ならもう言いたいことがお分かりかと思いますが、「ヒラメのベイトがイワシだけだといっても必ず誤差が付くからヒラメから他のベイトが出てきたとしてもそれは誤差で真の値はイワシだけだといいたいんじゃないのか?統計数学を悪用してポジショントークしようとしているだけじゃないか」と思われるかもしれませんがその通りです。
下の図の場合は真の値が「0」ですが、計測した値はバラバラです。

下の図はy=xが正しいモデル式

現実というのはたとえy=xが真実だとしてもy=x通りにはデータの値が出てくれないものなのです。多分。
もし「ヒラメのベイトがイワシだけ」というのが真実だとしても現実には「ヒラメの腹から出てくるのは イワシ+α(誤差)」でも問題はないと自分は思います。
相関関係で因果関係かどうかというような問題もあったりしますが、LiNGAMという新しい方法で因果と相関について勉強中です。
勉強は絶賛座礁中。
ベイトの話は僕のアンチの活性が上がってしまうのであんまりしないことにして、この誤差を考える時結構面白いなぁと思ったのが、
「ルアー釣りは魚の誤差」しか対象にしていないという事。
普通、世の中のものはなんでも「誤差を少なくする」ことに力を入れておりますが、ルアー釣りの場合は魚に餌じゃないものを食べさせる、という事をやろうとしているので、魚の習性+α(誤差)のα(誤差)だけでやる釣りです。
これがエサ釣りだと「魚の習性+α(誤差)」で釣りをするので現実的な釣りと言えます。
例えばヒラメにイワシの泳がせ釣りを使うのはイワシを追っているヒラメの本来の習性、それにもしかしたら糸に垂らされているイワシに対するなんらかの反応という誤差を含むので「現実=虚構+真実」ということになります(なると思います)。
youtubeで村岡さんの動画を観ていると「釣れるシーバスは数割」みたいなことを仰っていて、寧ろルアーでは釣れる方が誤差だと思います。
これはルアー釣りに大きなヒントになりそうな気がします。
例えば一つ仮定を立ててみる。
「魚が本来の習性が最大限の時(真の魚の習性からの誤差が小さい時)、ルアーでは釣れなくなる」
「一方、回遊から外れた魚、本来の海域にいない(誤差が大きくなっている時)魚はルアーへの反応がよくなる」
例えば、摂餌中の魚はルアーへの反応が鈍くなったりするけど、餌を食ってなくて何しているかちょっと分からないような魚は結構ルアーに反応がいい、というようなことが起きているのかもしれない。
この仮定が真なら、「ルアーで夜によく釣れる魚は昼行性」といえる。
「ルアーを噛むのは魚の習性を利用したもの」ではなく「魚の習性の誤差」という話だったのですが、反例(否定するような内容の例)となるような話では、弟の持っている本に「絶対口を使わない渓流魚に口を使わせるテンカラ釣りの漁師の秘伝の方法がある」との事。
洪水の時で魚が絶対に餌を食べない状態でも必ず釣って帰るという漁師さんがいらっしゃって、そういう方法があるみたい。
現実=誤差+真実なのに誤差の方がデカいのはおかしいからさっきの仮説が否定されてしまう。
結構飛躍した話になったけど、なんか面白そうなネタを得たので色々検証したいと思います。
- 2021年5月21日
- コメント(0)
コメントを見る
fimoニュース
| 16:00 | 釣り人なら皆やってる? ラーメンは… |
|---|
| 14:00 | 悪癖 やりたい釣りを迷う |
|---|
| 10:00 | 26フリームスと23レガリスをスペック比較 |
|---|
| 08:00 | 釣り人も多く嫌う人もいるけれど…バチ抜けは楽しい |
|---|
登録ライター
- ムスッとしてたら
- 1 日前
- はしおさん
- ヨーヅリ:トビマル
- 1 日前
- ichi-goさん
- 『ワームの釣りは、向い風が吉…
- 3 日前
- hikaruさん
- 44th 早い話がイマジネーション
- 9 日前
- pleasureさん
- フィッシングショー大阪2026行…
- 20 日前
- ねこヒゲさん
本日のGoodGame
シーバス
-
- '25 これぞ湘南秋鱸、大型捕獲♪
- ハマケン
-
- 流れの釣り
- Kazuma

















最新のコメント