日本海サーフでは海が凪過ぎると嘆く人と太平洋側では荒れすぎていると嘆く人が居ます。

凪と荒れ、どっちも嘆かれていますが、もしかしたらサーフフィッシングには波の高さは最適解のある問題なのかも、と思いました。

そこで分析をした結果、結論として先に書いてしまいますが、「予報で１ｍ以下に最適解がありそう」と思いました。


結構時間かけて分析をやったので記録として読んでいただけると幸いです。


以下はその方法です。（難しい話も出てきます）

まず、ひらめっぱりさんから取得した茨城の釣果、2260匹のヒラメの釣果とその時に釣れた波の高さのデータを図示します。


波の高さは記載されていなかったので犬吠埼の波の高さを５年分データに書き込みました。



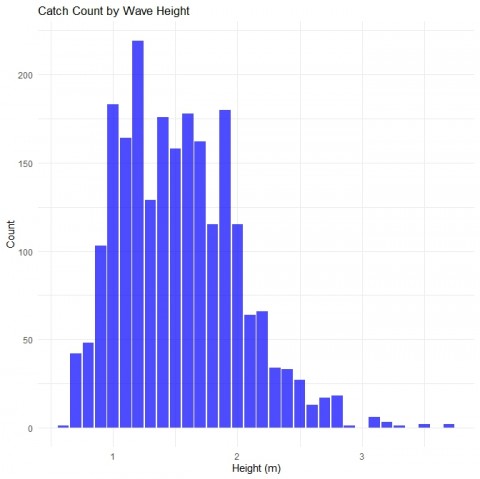
横軸は0.1m刻みなので一番釣れているのは1.2mですが1~2mの間であれば大体同じくらいに釣れています。

これを見て思ったのは、「ホントかよ」でした。

２ｍの波というとかなり釣りづらい感じがします。

原因として簡単に予想がつくところで、鹿島灘の波が高い日が多いから釣れた数も多いのでは？と思いました。

そこで波の高さの分布を調べました。


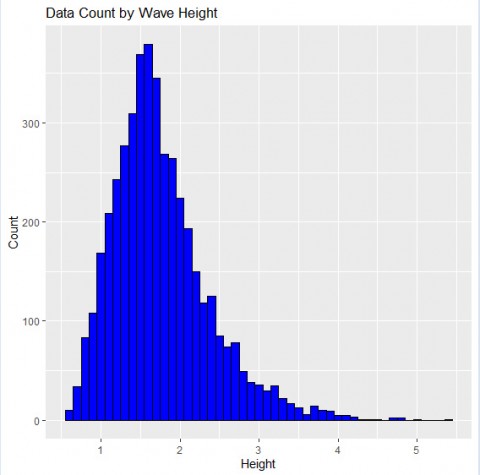
横軸は波の高さ。縦軸がその波の高さの日数。


鹿島灘は1.5mくらいの時の波の日が一番多い事が分かります。

ですので1.5mの日が多いので釣果もそれに引っ張られている可能性が有ります。




このグラフを見ると知っている人は知っているかもしれませんが、「対数正規分布」というものに従っていると予想されました。

単語自体を憶える必要はあまりないかもしれませんが、対数正規分布は日常のあらゆるところに潜んでいますので勉強してみるのもいいかもしれません。

典型的にはお金持ちの人数や売れ筋商品とその他の構成割合などで出てきます。

それとみんな大好きな「株」。


話を戻すと、確率で割り戻しするのにその日の波の高さの確率を知る必要がありますので対数正規分布からその確率を求めます。

この波の高さが対数正規分布に属しているかどうかをKS検定を使って調べました。

対数正規分布についての参考のwikipedia。
https://ja.wikipedia.org/wiki/%E5%AF%BE%E6%95%B0%E6%AD%A3%E8%A6%8F%E5%88%86%E5%B8%83

KS検定の結果、対数正規分布が一番可能性として高かったので、とりあえずフィッティングしてみました。

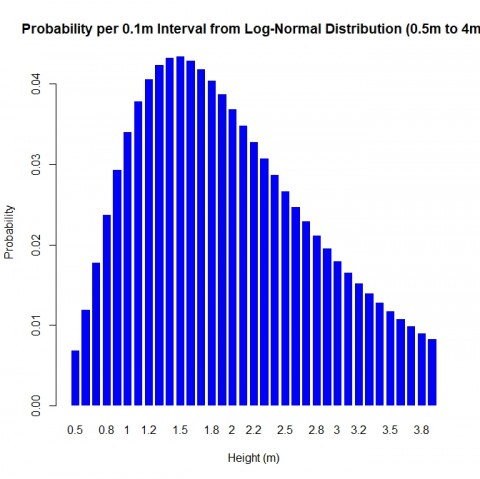
途中までしかないですが、ロングテールの部分は釣果がないために端折りました。（記事を書いている時に、じっくり見て見るとフィッティングが上手くいっていないような感もあります。最大値は殆ど同じだし、実際の減衰がもっと激しい感じではありますが、大幅に間違ってはいないだろう、と思います。）

ここからハイパーパラメーターチューニング（かっこいい名前）を行って、0.1ずつ分散を調整して一番あてはまりのいい対数正規分布を求めました。


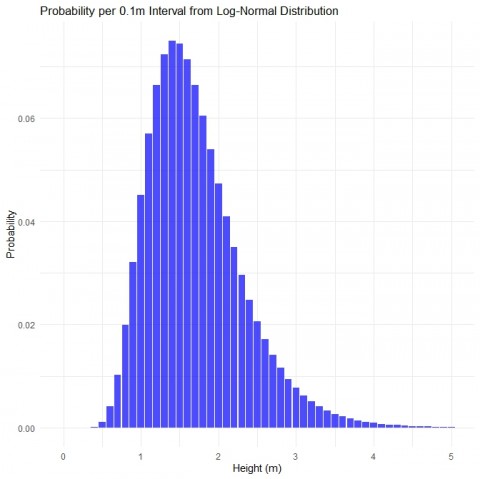
さっきの波の図と大分近くなりました。


これによって波の分布の確率が求まったので、釣果を割り戻ししたいと思います。

それがコレ。



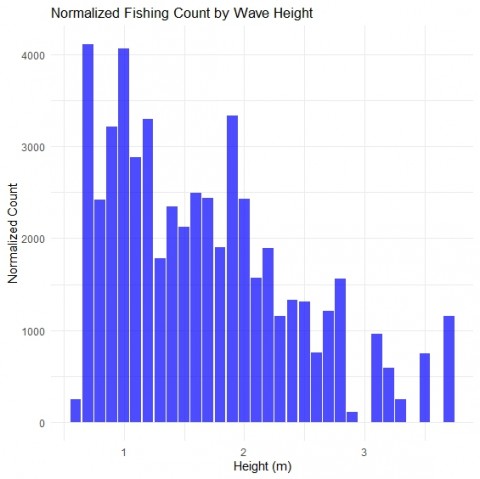
あまりきれいな図にならずに残念ですが、波が高くなれば減衰しているのは分かります。

図の解釈：横軸は波の高さで0.1m刻みです。

縦軸は規格化した釣果数です。

規格化した釣果数というのは波の確率で釣果を割ったものです。

例えば、波の高い日と低い日が90%と10%でその釣果が５；５だとすると5/0.9=5.55と5/0.1=50が規格化された釣果数です。

この場合は圧倒的に波の低い日の方が釣れやすいと解釈します。


グラフの観察に話が戻りますが、最初の予想だと凪過ぎても荒れすぎていてもダメなのでは？と思っていましたが、そういうものがあるとしたら0.6m~１ｍの範囲ぐらいにその可能性を感じます。

ここで、線形回帰分析とガウス関数の極値（最適な波の高さがあると仮定したため）を持つタイプの減衰型とでフィッティングして比べたところ、さすがにガウス関数の方が当てはまりが良かったですが、それはわずかでした。

要するに、最適な可能性はわずかにある、といった感じです。

P値は統計的に有意ではありました。

モデルというのは複雑にすると当てはまりが良くなるので確実にあるとは言えないでしょう。（無いとは言えないです）
　
ちょっと話はズレるのですが、社会科学の論文なんかではこのくらいの解釈で～という事が判明みたいに書いてあったりしますが、釣りはかなり厳密に議論されている事が多いので下手な事を書けないのでこのくらいの書き方に致しました。

反省と考察

反省点としては日曜日は人が多いので釣果が多い傾向がありますから、日曜日の釣果も正規化してやる必要を感じました。

今回の結論としては、予報で0.6~1mくらいの間に何かしらの最適解がありそうだ、くらいの結論になりそうです。

波が0.5mだとあまり釣れてない点が一点あるところが怪しくはあります。

もし最適解があるとしたら、「流れの速さ」が釣れる理由になっているという事が挙げられます。

考察が自分の理論で恐縮ですが、イワシはサーフには用があって回遊して来ているわけではなくて波によって流されてやってくる、と思っています。

しかし、流れが速すぎると魚が散るのが早くなるので釣れ無くなる、と予想を立てています。

イワシが流される限界というのがあってそれ以上になると段々釣れ無くなる、という結論は否定はされないものの、強くは肯定はされない（微弱）くらいの印象です。

もし今回のグラフのデータがキレイだったら波の高さだけで釣果が予想できてしまうので分析が上手くいかないのも良かったかなと思いました。

最後に

これからも素人ながらデータサイエンスを勉強して分析して記事にしていきたいと思います。


お精読ありがとうございました。