フックの法則は、中1の理科で習うようですし、以下にお示しするf＝kxと言う式でさえ、高校の物理で習う内容です。

運動方程式も同様です。

公式、２つしか出てこないので、ぜひご理解頂けますと！！

ご理解頂いてる方には、釈迦に説法ですが、文系の方や、理系で習ったけど忘れちゃったよ、と言う方にもわかりやすいように心がけて書きましたので、

非常にまわりくどく、同じことを何度も言ってるかもしれませんが、ご容赦ください。

そもそも、とある実験結果に対する考察のお話でして、『糸の長さが長くなると？、単位m当たりの負荷が分散される云々』と。

この分散云々を前提に考察されたのであれば、それは間違っていますよ、というご指摘をさせて頂いたのです。

極めて丁寧に。

で、僕のように誤解する方が出て来ないよう、たくさん追記をしてくださったのですが、そもそもの理解の仕方が違うので（現時点ではどちらが正しいとか、どちらが間違っている、とかではなく、これを読んだ方がご判断頂ければ良いと思います。）、追記のところにも矛盾点、僕と違った理解をされている点がありますので、僕の考えを述べさせて頂こうかな、と。

僕がやろうとしていることは、実験、ではなく、証明、と言えるかと思います。

具体的な状況に添って、公式に具体的な数字を代入して、となると思います。

糸が伸びた状態で、アタリが伝わるかどうかのお話もされていますが、それはまた別の話で、弦の固有振動数とかの話にもなってくるので割愛します。

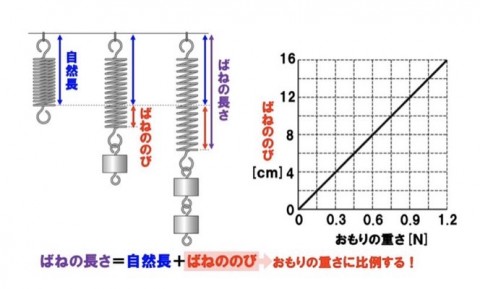
まず、フックの法則です。

ネットでの拾い物の画像を添付した方がわかりやすいので、ご容赦ください。

ばねの直列つなぎ

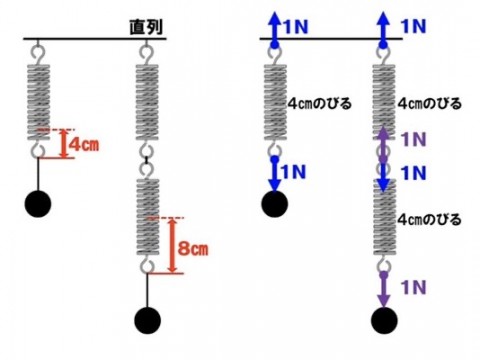
これも、張力はどこでも一定、を理解していないと理解できないのでw

並列つなぎもあるんですが、今回のテーマとは関係ないし、混乱しちゃうので割愛します。

次に1番大事な公式、Wikipediaより、

ばねと、釣り糸は違うじゃん、も思われるかもしれませんが、釣り糸も、フックの法則（弾性の法則）に従います。

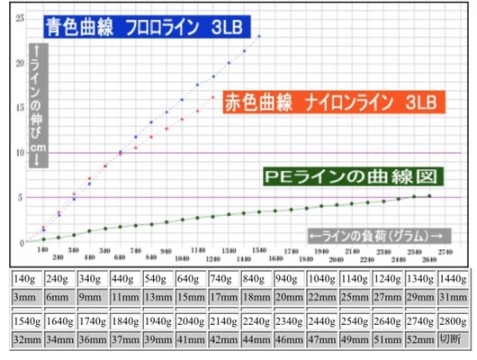
これは、実際実験されている方がいて

見事な比例関係！

糸にかかる重さに比例して、伸びている事がおわかり頂けるかと。

即ち、釣り糸はフックの法則が成り立つ、とご理解ください。

破断強度近くだと成り立つ？成り立たない？とか言ってる人もいましたが、上のグラフが途切れてるところは、糸が切れた重さなので、軽い負荷から、切れる寸前まで、比例関係が成り立っている事がご理解頂けるかと。

F(N)＝ｋ(N／ｍ)×ｘ(m)ですが、N(ニュートン)という単位はとっつきにくいので、このブログ内に限っては

見慣れた単位で統一して

F(㎏)＝k(㎏／㎝)×ｘ(㎝)としましょう。

（あちらの、僕自身のコメントで、長い糸は伸びやすい、は間違っている、と言ってしまいましたが、上記のように、同じ糸であれば、長い糸は伸びやすい、と言えます。お詫びして訂正させて頂きます。）

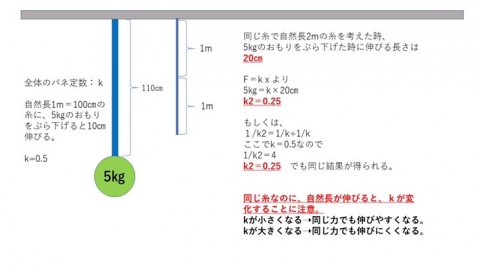
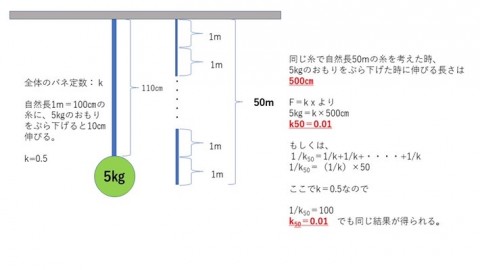
とある考察の中にあるように、自然長100センチの糸に、5㎏のおもりをぶら下げると、10センチのびるとします。

Ｆ＝ｋｘなので、

5＝ｋ×10

ｋ＝0.5です。

kは大きくなるほど伸びにくく、

kは小さくなるほど伸びやすいと言えます。

あちらでは伸び率10パーセント、みたいないい方をされていましたが、そもそもそれがまちがいなのかな、と。

フックの法則は、重さに比例してバネも比例して伸びる、ということですからね。

そして、もう一つ話をややこしくしてるのは、バネでいう自然長=糸の自然長もいつも同じとは限定していないことです。

たとえば、リーダー1メートル、とメインライン50メートル、とかね。

同じ糸で、同じ負荷であれば、糸の長さに関わらず、張力が一定、とか、フックの法則を正しく理解していないと、混乱してしまうのでしょうね。

この糸に5㎏の負荷をかけたとき、これは比例の式で解いたほうがわかりやすいので、

200センチの糸なら、

100：10＝200：□センチ、なので、□＝20センチになります。

200センチなら20センチ

300センチなら30センチ

50メートルなら5メートル伸びます。

5㎏の負荷なら自然長の10パーセントの伸び、で正しいのですが、

この糸1メートル(100センチ)に下記の負荷をかけたとすると

Ｆ＝ｋｘより、このいとではｋ＝0.5ですから、ｘ＝Ｆ／0.5より

1㎏なら2センチ、2パーセントの伸び率

2㎏なら4センチ、4パーセントの伸び率

3㎏なら6センチ、6パーセントの伸び率

4㎏なら8センチ、8パーセントの伸び率

5㎏なら10センチ、10パーセントの伸び率

この通り、同じ糸で、10パーセントの伸び率、という考えがまず、間違っている、ということがお分かりになるかと。

そして、10㎏なら20センチのびて(20パーセントの伸び率)、10㎏より少しでも負荷がかかると、糸がきれるとしましょうか。

ここで勘違いされないようにあえて申し上げておくのですが

200センチの糸に5㎏のおもりをぶら下げて20センチ伸びているのと(敢えて言えば10パーセントの伸び率)

100センチの糸に10㎏のおもりをぶら下げて20センチ伸びているのとでは(20パーセントの伸び率で、切れる寸前)、

おなじ20センチの伸びでも意味がちがうということです。

同じ糸なのに、長さによってkが変化することをご理解ください。

さて、どこかの設定通り、竿を1メートル煽る？としましょう。

グレーの棒を竿だと思ってください。

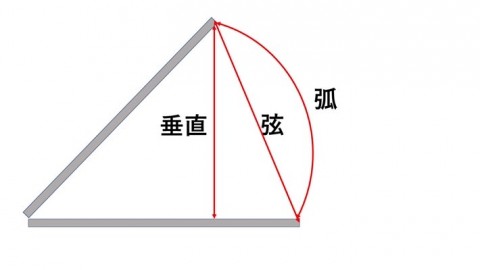
孤の長さを1メートルとするのか、

弦の長さを1メートルとするのか、

垂直に1メートルなのかはわかりませんが、

ここはわかりやすく、1メートル竿を垂直に持ち上げる、としましょう。

硬くて、曲がらない棒のような竿です。

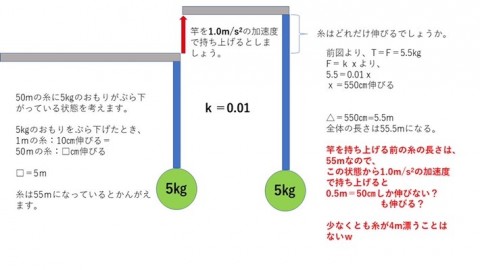
この時、②糸に既に５キロの負荷がかかっている状態から竿を1メートルあおったのか、

①負荷ゼロの時から、竿をあおったのか、

僕には読解できなかったので、両方の状態について考えてみます。

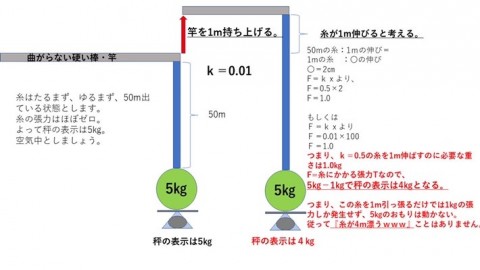
まずは、①竿をあおる前の糸の負荷がゼロ、の状態を考えます。

わかりやすく、空気中での話として、重りの下に秤を置いてみます。

（赤字の部分、k＝0.5の糸を・・・の0.5は間違いです。k＝0.01がただしいです。計算は間違って無いので、ご安心を）

５キロの負荷をかけるつもりで？1メートル、竿を持ち上げたとしても、実際に糸にかかる負荷は、1キログラムしか掛かっていない事がわかります。

５キロ負荷をかけたいなら糸の伸びぶん5メートル竿を煽るか、リールを巻かないと、５キロの負荷はかかりません。

当然、糸が4メートル漂ったり、どこかに消えることはないですね。

そもそも、張力は、糸がたるんでない限り一定、と言う規則ですから、漂うwとか言ってる時点で、張力について誤った理解をしてらっしゃるんですよね。

はい、次。

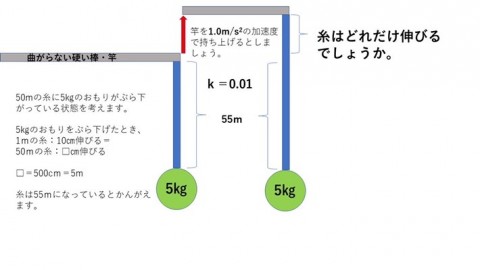
②糸に５キロの負荷がかかってる状態から1メートル竿をあおることを考えます。

これは、この後お話しする運動方程式ってのが関係してきます。

重要なのは加速度、です。

どれだけのスピードで、と言うか、どれだけの加速度で竿を煽ったか、が関わってきます。

逆に言うと、ものすごーーくゆっくり竿をあおれば、糸にかかる張力は一定のまま、糸は伸びることも、切れることもなく、５キロの重りを動かす事ができます。　

これも、どれだけの加速度であおったか、は言及しておりませんので、こちらで数字を代入して考えます。

この後出にてくるのは運動方程式です。

運動方程式では、重力加速度が定数で入ってきてしまうので、どうしてもＮ：ニュートンと言う単位を使わざるをエマワトソン！

運動方程式、糸の持ち上げ、などで検索してみてください。

計算しやすく、糸は伸びないもの、と仮定している例題が多いですが、伸びる糸でも成り立ちます。

糸に５キロの重りがぶら下がって、50メートルの糸が、伸びて55メートルになっている状態で、上記の加速度で持ち上げると、糸は50センチ伸びるという事がわかります。

これも、少なくとも、糸が4メートル漂うwことはないです。

違う加速度で考えてみます。

竿をあおる加速度を上げていきます。

10キロ以上の負荷が掛かれば切れる糸、と定義しているので、a＝10で、糸にかかる張力が10.1となり、切れる事がわかります。

この時、糸は瞬時に10メートル伸びている事になるので、現実的ではないかもしれません。

ちょっと前に書いたのですが、出来るだけゆっくり竿をあおる、つまりa＝0になるようにゆっくり竿を持ち上げれば、糸の張力はほぼ変化することなく、5キロの重りを引っ張る事ができます。

加速度、というのがとっつきにくいのですが、

飛行機を考えてみてください。

離陸時、飛行機は物凄い加速度で運動していますから、

飛行機の進行方向とは逆向きの力、即ち、

シートに僕たちの体が押しつけられる方向に力が働くのです。

予定高度に達して、水平飛行している際は加速してないので、シートに体が押しつけられることもなく、自由に動けるわけです。

実は飛行機は加速してるのですが、空気抵抗と加速度が釣り合って、加速度が打ち消されているのです。

加速度を持たない物体には力がかかっていない、と理解されます。

雨粒も、落ちていく重力加速度と、空気抵抗が釣り合っているので、見かけ上、力は働いてない、と理解されています。

むずかしいですね。

3月5日18時45分追記

つまり。

糸にぶら下がっている重さに関わらず、

すげー早く糸を持ち上げようとすれば、加速度aがデカくなれば、糸に過大な張力がかかって切れやすくなる（もしくは伸びる）。

どんなに重い物がぶら下がっていても、

すげーゆっくり、加速度をなるべく0に近づけるように動かせば、糸は切れることなく、張力を保ったまま、重りの重さと釣り合ったまま、重りを釣り上げる事ができる。

ただし。

こちらがいくらどんなにゆっくり引っ張ったとしても、

相手が魚だった場合、急にダッシュをする＝糸に急な加速度がかかる→伸びきって切れる、となるわけです。

そもそも、

こーゆー子供がやるような引っ張り合いの話のはずだったのに、いつのまにか細糸での魚とのやり取りや、フッキングの話とかを出してこられて、必死だなぁ、と。

①細糸であっても、張力が釣り合って、加速度が小さくなるように引っ張れば、寄せてこれますよね。

ただ、細い糸であればあるほど、人間側が引っ張るわずかな加速度で、

細糸にとっては大きな張力がかかってしまうのと、

魚のわずかなダッシュ＝加速度で張力がかかってしまうので、やり取りが難しい→記録になるわけで。

②P Eでも、ナイロンでも、張力は一緒ですので、同じ力をかけることができますよ。

フッキングにかかる力を提示されていなかったので、仮に、シーバスの口にフッキングさせるのに必要な力を5キログラムとしましょう。

ナイロンは、ここまで使ってきた糸の設定にしましょう。

50メートルで、5キロの負荷で、5メートル伸びる糸。

PEは、伸びにくいので、

50メートルで、5キロの負荷で、1メートルしか伸びないとしましょう。

ナイロンは、50メートルの状態から55メートルになってますから、5メートル巻き取れば5キロの負荷がかかります。フッキングできます

P Eは、50メートルの状態から51メートルになってますから、1メートル巻き取れば5キロの負荷がかけられます。フッキングできます。

同じ負荷をかけるのに、伸びる長さが違うので、巻き取る長さが違う→巻き取る時間が違う、と言うだけです。

糸によって、かけられる負荷が違う、わけではないですね。

そして、今回運動方程式を眺めていて、ある事に気づきました。

タックルで凧揚げ、の話です。

凧が糸を引っ張る力と、

糸の張力が釣り合っていて、

ドラグも出ていかない状態を考えます。

ここで、凧を動かそうと、勢いよく竿をあおると

→糸に加速度がかかります

→伸びる糸だと、加速度分は糸が伸びる力に使われてしまって、凧はぜんぜん寄ってこない、動かない！と言うことなんですね。

従って、凧を動かそうとするならば、出来るだけゆっくり、加速度がかからないように糸を引けば、凧はじわーーっと動くはずですね！

ただ、そこで、突風が吹けば、糸が切れたり、凧が離れていってしまうのは、魚とのやり取りと同じです。

糸の張力、フックの法則、運動方程式、とっつきにくいかもしれませんが、これらを理解することで、タックルで凧揚げ、の理論もなんとなく理解できました！

いやー、物理も知ってて、釣りも知ってる人ってのがいなくて、相談する人もいなくて、疲れましたw

パワポでスライド作るのに、仕事の合間を使って3日くらいかかっちゃいました。

どちらが正しいか、間違っているか、ではなくて、

どんな理論に基づいて、ある事象を見ているか、の違いですので、その辺りのことをご理解ください。