■はじめに
こんにちは、わさびです。
前回は、ジャークについての深堀りをしました。
今回も引き続きジャークについての深堀りをしていきます。
もしも疑問点やご質問があれば、是非ともコメントしていただければ幸いです。

なお、前回の記事について、誤字脱字と一部数式の修正をしております。
数式については、具体的には、ルアーのアイの位置（縦方向）y2をHと表現していましたが、正しくは-Hなので、修正しました。
手の位置を原点（0, 0）にしているため、手より下の座標はマイナスになります。
今回の記事では、符号（プラス / マイナス）が重要になるため、前回の記事を修正するに至りました。
計算結果の数値が変わるわけではございませんが、是非ともご確認よろしくお願いいたします。
 

---

■ジャークについて
それでは、今回もジャークについて深掘りしていきます。
よろしくお願いします。

●ジャークについてどうアプローチするのか
前回は、ウェーディングの状況を想定して考えてみました。
具体的には、ロッドをジャークするときの回転軸（ロッドの後端）が水面と同じ高さであることを仮定して計算しました。
今回は、堤防や地磯での釣りを想定した計算を行います。
具体的には、ロッドをジャークするときの回転軸（ロッドの後端）が水面よりも高いことを仮定して計算します。
計算の過程は、前回との差分だけを説明して、それ以外は割愛させていただきます。

●地磯や堤防でのジャークについて
図1は、今回の計算するにあたり作成した概念図です。
地磯・堤防に釣り人がいて、キャストしたルアーを巻き取りながらジャークすることを想像してください。



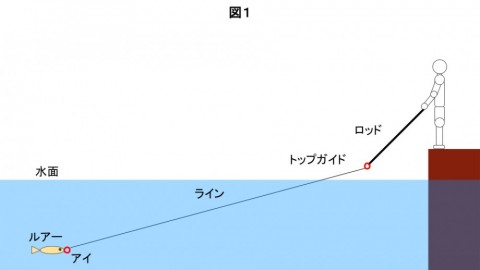
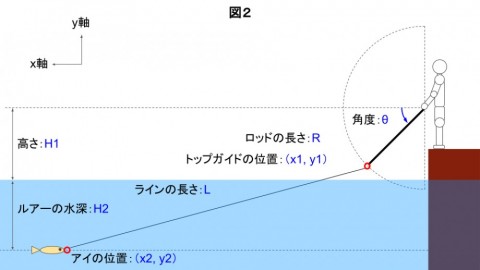
図2は、ロッドを角度θの方向にした状態のルアー位置を計算するためのものです。
計算するために、いくつかの変数を定義しておきます。
ロッドの長さ：R
ロッドの角度：θ
トップガイドの位置（横方向）：x1
トップガイドの位置（縦方向）：y1
ラインの長さ（≒ キャスト距離）：L
水面から手まで高さ（≒足場の高さ）：H1
ルアーの水深：H2
ルアーのアイの位置（横方向）：x2
ルアーのアイの位置（縦方向）：y2



計算方法は前回と同じなので、割愛させていただきます。
前回の記事を参考に、トップガイドの位置（x1, y1）を求めてから、ルアーのアイの位置（x2, y2）を求めてみてください。
計算のポイントや、前回との違いを少しだけ説明させていただきます。
計算における原点は、前回と同様に手の位置であり、座標（0, 0）とします。
ロッドの角度は、真横（9時の方向）を±0°とします。
上（12時の方向）を+90°とし、下（6時の方向）を-90°とします。

トップガイドの位置は、前回同様に以下の通りです。
x1 = R × cosθ
y1 = R × sinθ

ここで、少し補足です。
例えば、ロッドを12時の方向にした場合、角度θ = 90° なので、
y1 = R × sin(90°) = R
となります。
手（原点）より上方向にRだけ離れているということです。
ロッドを6時の方向にした場合、角度θ = -90° なので、
y1 = R × sin(-90°) = -R
となります。
手（原点）より下方向にRだけ離れているということです。

ルアーのアイの位置は、前回記事の数式に、水面から手までの高さH2を加えたものになります。
すなわち、前回記事の数式のHをH1+H2で置き換えたものと等しくなります。
x2 = √(L^2 - (H1+H2+y1)^2) + x1
y2 = -(H1+H2)

以上で計算式は出せました。
詳細は割愛させていただきましたので、もしも疑問点やご質問、ご要望があれば、是非ともコメントで教えてください。
よろしくお願いいたします。

次に、前回と同じように、計算式に具体的な数値を当てはめていきます。
いくつかの項目に分けて、具体的な数値の計算と考察をしていきたいと思います。

●ジャーク角度を変えてみた
下記仮定のもと、ジャーク角度に対応するルアー位置を計算しました。
なお、ルアー位置は横方向のx2だけを示します。
ロッドの長さ：9 feet
ラインの長さ（≒ キャスト距離）：70 m
水面から手まで高さ（≒足場の高さ）：3 m
ルアーの水深：3 m

ジャーク角度 vs ルアー位置
-90°のとき：69.92 m
-60°のとき：71.28 m
-30°のとき：72.22 m
0°のとき：72.49 m
30°のとき：71.99 m
60°のとき：70.87 m
90°のとき：69.45 m

ロッドを9時の方向から12時の方向に立てるほど、ルアーが手前に来ます。
同様に、ロッドを9時の方向から6時の方向に寝かせるほど、ルアーが手前に来ます。

ジャークをする際、堤防等ではロッドを19時くらいの方向から20時くらいの方向に動かすことが多くないでしょうか？
今回の計算結果だと、上記の要領でジャークした際に、ルアーを引くことができません。
むしろラインが緩んでしまうため、ルアーが動かない（または離れてしまう）ような計算結果になります。
ここで、現実的なことを少し考えてみましょう。
そもそも、ラインは常に直線ではなく、多少たわんでいます。
潮の流れやルアーが自重で沈んでいくことも考慮すると、やはり今回の計算で正確なルアーの動きを表現することはできないのだと思いました。
そうだとしても、思考停止してしまうとそれまでです。
まずは今回の計算式を使って、他の数値も見てみたいと思います。

次に、ロッドの角度を30°ずつ変えたときに、ルアーがどれだけ移動しているのかを、上記数値の差分から見てみました。
-90° → -60°のとき：-1,353 mm
-60° → -30°のとき：-995 mm
-30° → 0°のとき：-263 mm
0° → 30°のとき：499 mm
30° → 60°のとき：1,118 mm
60° → 90°のとき：1,417 mm

ロッドの角度を0°から90°に向かって立てる場合は、ルアーの移動量が大きくなります。
これは、前回の記事と同じ動きですね。
ロッドの角度を-90°から0°に向かって立てる場合は、ルアーの移動量がマイナスになります。
また、ロッドの角度が-90°（6時の方向）に近いほど、ルアーの移動量が大きくマイナスになります。
ルアーの移動量がマイナスということは、図2で言うと、ルアーが左側に動くことになります。
水流や自重で沈むことがないと仮定すれば、ルアーの位置は変わらずに、ラインがたわむことになります。
この記事の中では、ルアーの移動量がマイナスになった際に、ラインがたわむと表現することが多々あると思います。
ご理解いただけると幸いです。

上記計算がどこまで合っているのかを検証する方法を考えてみました。
ロッドを-60°の位置で固定して、リールを巻いてラインを張ったとしましょう。
そこから-30°に向かって上方向にジャークしたときと、-90°に向かって下方向にジャークしたとき、それぞれでルアーはどう動くでしょうか。
前者よりも後者の方がルアーの動きが大きい場合は、今回の計算結果が”傾向”として合っていることになります。
ただし、ルアーの動きを目視で確認することは難しいですよね。
そこで考えているのは、動きが大きめのミノーを使うことです。
ブルブルとしたミノーの振動を、どちらの方が大きく感じることができるのかを確認してみたいと考えています。
計算の傾向が正しければ、ロッドを-60°から-90°の下方向にジャークした方が、振動が大きくなると思います。
足の怪我が治ったら、自分で試して皆様にもご報告させていただきます。

●ロッドの長さを変えてみた
下記仮定のもと、ロッドの長さに対応するルアー移動距離を計算しました。
なお、ルアー移動距離は横方向だけを示します。
ジャーク角度：0° → 30° と -60° → -30°
ラインの長さ（≒ キャスト距離）：70 m
水面から手まで高さ（≒足場の高さ）：3 m
ルアーの水深：3 m

ロッド長さ vs ルアー移動距離（0° → 30°）
7 feet：386 mm
8 feet：422 mm
9 feet：499 mm
10 feet：556 mm

ロッド長さ vs ルアー移動距離（-60° → -30°）
7 feet：-730 mm
8 feet：-837 mm
9 feet：-945 mm
10 feet：-1,053 mm

0° → 30° の場合、ロッドが長い方が、ルアーの移動距離は大きくなりますね。
同様に、-60° → -30° の場合では、ロッドが長い方が、ラインのたわみが大きくなりますね。
どちらにおいても、ロッドの長さに対して影響度は大きくないように感じます。

●ラインの長さ（≒ キャスト距離）を変えてみた
下記仮定のもと、ロッドの長さに対応するルアー移動距離を計算しました。
なお、ルアー移動距離は横方向だけを示します。
ロッドの長さ：9 feet
ジャーク角度：0° → 30° と -60° → -30°
水面から手まで高さ（≒足場の高さ）：3 m
ルアーの水深：3 m

ライン長さ vs ルアー移動距離（0° → 30°）
70 m：499 mm
50 m：553 mm
30 m：681 mm
10 m：1,610 mm

ライン長さ vs ルアー移動距離（-60° → -30°）
70 m：-945 mm
50 m：-921 mm
30 m：-865 mm
10 m：-548 mm

0° → 30° の場合は、前回の記事と同じで、ラインが短くなるほどルアーの移動量が大きくなっています。
それに対して、-60° → -30° の場合では、ラインが短くなるほどにルアーのマイナス方向の移動量、つまりラインのたわみ量は小さくなっています。
一瞬混乱してしまうかもしれませんが、ラインのたわみ量が小さくなるということは、ルアーを釣り人側に移動させようとする方向に数値がシフトしているということです。
図2を見ながら考えてみましょう。
現在の位置からのルアーの移動量が-1,000mmだと、大きく左に移動するイメージです。
ルアーの移動量が-100mmだと、小さく左に移動するイメージです。
両者を比較すると、相対的には右側に移動していることがわかると思います。
つまり、ロッドをどの角度でジャークしたとしても、ラインが短くなるにつれて、ルアーを手前に引く力が強くなると考えられます。

●水面から手まで高さ（≒足場の高さ）を変えてみた
下記仮定のもと、ロッドの長さに対応するルアー移動距離を計算しました。
なお、ルアー移動距離は横方向だけを示します。
ロッドの長さ：9 feet
ラインの長さ（≒ キャスト距離）：70 m
ジャーク角度：0° → 30° と -60° → -30°
ルアーの水深：3 m

水面からの高さ vs ルアー移動距離（0° → 30°）
0 m：440 mm
3 m：499 mm
6 m：559 mm
9 m：620 mm

水面からの高さ vs ルアー移動距離（-60° → -30°）
0 m：-988 mm
3 m：-945 mm
6 m：-901 mm
9 m：-857 mm

9mの差があっても、ルアーの移動量は180mmしか変わらないという結果になりました。
今回の計算で仮定した条件においては、水面からの高さ影響も小さそうですね。
ただし、ラインの長さ（≒ キャスト距離）が短くなると、影響が大きくなるような気がします。
なぜなら、ルアーを引こうとする角度が大きくなるからです。
あくまでイメージになってしまいますが、0mだと真横からルアーを引くことができるとしたときに、9mだと45°やもっと上からルアーを引くようになると思います。
この角度の違いが、ライン長さが短くなる方が顕著になると思います。
細かい数値については、また次回に深堀りしてみたいと思っています。

●総括
ロッドを0°から90°の方向にジャークする場合は、ルアーを回収する方向に力が働く。
ロッドを-90°から0°の方向にジャークする場合は、ラインがたわむ方向に力が働く。
ラインの長さ（≒ キャスト距離）が短いほど、ジャークによってルアーを手前に引く（回収しようとする）方向に働く力が大きくなる。
水面から手まで高さ（≒足場の高さ）の影響は、ラインの長さ（≒ キャスト距離）が長い場合には小さい。
 

---

■最後に
今回も、前回に引き続きジャークについて考えてみました。
ロッドの角度がマイナス方向（下向き）になると、同じように上方向にジャークしたとしても、ラインがたわむことを発見することができました。
しかし、自身の経験として、ラインがたわむような感覚はなかったので、実際にラインがたわむとは考えられません。
とはいえ、ロッドを上向きではなく、下向きにジャークすることでルアーの動きが大きくなる可能性はあります。
この記事の途中で触れましたが、海で実際に検証することが楽しみです。

前回の記事では、算数・数学的な内容をご理解いただけたというコメントも頂くことができて、僕自身もとても嬉しかったです。
頑張って記事を書いてよかったと思えました。
一方で、理解できずに「う〜ん」といった感じの方も多いのかなと予想しています。
数式というよりは、考え方をご理解いただき、そこに少しでも面白さを感じていただければと思います。

次回は、前回と今回の記事の内容を、数値的に噛み砕くことができるようにしたいと思います。
具体的には、ロッドの長さ等の様々なパラメータを変えたときに、ルアーの移動距離がどうなるのかをグラフとして示していければと思います。
Excelを使ってたくさん計算して、グラフを描いて、解説していきたいと思います。
数式と違い、目で見てわかりやすいと思いますので、是非とも次回の記事も読んでいただければ幸いです。

最後まで読んでいただきありがとうございました。
次回も引き続き、ジャークについて深堀りしてみたいと思います。
よろしくお願いいたします。