■はじめに
こんにちは、わさびです。
前回は、リールのギア比についての深堀りをしました。
自分でいろいろ調べたり計算するのは面白かったです。
今回は、ジャークについて深堀りしてみます。
1週間かけていろいろと調べたり考えてみましたが、計算で表すことが難しかったです。
本当にこの計算でいいのか？そもそも、この動きは計算できるのか？などなど。
結果として、ある程度の仮定（縛り）を設けて、かつ無理な計算は省くことで、なんとか形にすることができました。
前回よりも計算量が多く、内容も少し難しくなってしまいました。
計算をしているものイメージをしやすいように、図も用意してみました。
わかりにくい点も多々あるかと思いますが、是非とも読んでいただけると嬉しいです。
気になること等があれば、是非ともコメントしていただけると幸いです。
 

---

■ジャークについて
今回、ジャークについて深堀りする前に、そもそもジャークとは何なのかを調べてみました。
「リールを巻きながらロッドをあおるようにしてルアーをスライドさせるテクニック」とのことです。
自分なりに、以下の動きをイメージしてみました。
１．ロッドを寝かせた状態でリールを巻く
このときに、ある一定の速度でルアーが動きます。
これ以降、リールはずっと一定速度で巻いていると仮定して話します。
２．ロッドを立たせる（ジャーク①）
このとき、ロッドを立たせたことで、勢いよくラインを引くことになります。
そのため、ルアーは高速で動きます。
また、上方向にかかる力が強くなるため、角度やルアーによってはルアーは斜め上に移動します。
リップ付きのミノーであれば、水深を維持するように真っ直ぐと進むと思います。
３．ロッドを寝かせる（ジャーク②）
このとき、ラインにたわみができます。
ラインのたわみをリールが回収できるまでの間、ルアーは自由な状態になります。
基本的には、フリーフォールになると考えています。
ただし、ルアーも急には止まれません。
ジャーク①の動きが慣性で残っていることも考えられます。
したがって、ジャーク①でルアーにかかった力が水の抵抗によって完全に打ち消された後に
フリーフォールが始まると考えられます。

●ジャークについてどうアプローチするのか
この記事のポイントになるのは、ジャークをどう考えていくかです。
さまざまな視点があるとは思いますが、「ルアーがどう動くのか」に着目して考えてみました。
とはいえ、専門家でもなく、シミュレーションソフトがあるわけでもないので、複雑な動きを計算することはできません。
今回は、ジャークの動き、もっと言えば、ロッドを寝かせた状態から立たせたときに、ルアーがどのくらいの距離を移動するのかについて、計算してみました。
ルアーの移動距離がわかれば、ジャークの時間で割ることで、ジャーク時のルアー速度が求められます。
また、ルアーの移動距離＝ラインのたわみ量と考えることができるため、これをもとに次回はさらなる深堀りをしていきたいと思っています。
また、計算をするにあたり、以下の２つのシチュエーションで考えてみました。
① ウェーディング
② 地磯や堤防

この記事では、ウェーディングについてご説明させていただきます。
自磯や堤防については、次の記事でご説明できるように頑張ります。

●ウェーディング時のジャークについて
それでは早速、計算するための仮定を説明させていただきます。
図1は、今回の計算するにあたり作成した概念図です。
ウェーディング中の釣り人がいて、キャストしたルアーを巻き取りながらジャークすることを想像してください。



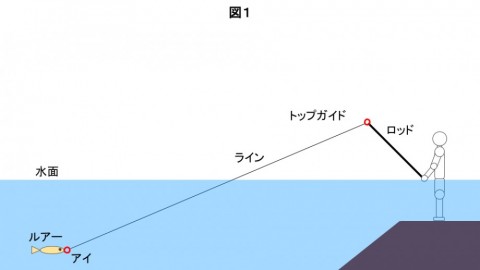
図2は、ジャーク時のロッドとルアーの動きを説明しています。
ロッドは、9時の方向から12時に向かってジャークすること仮定します。
また、ルアーはリップ付きのミノーであり、常に同じ水深を維持して進むことにします。
この仮定がないと、ルアーの動きを計算することができませんでした。
申し訳ございませんが、ご容赦いただければと思います。
計算では、トップガイドからルアーのアイまで、ラインが一直線に伸びていると仮定します。
これにより、ジャーク時のルアーの動きを幾何学的に計算することができました。
中学生の頃、数学で「この図面のこの辺の長さを求めよ」みたいな問題があったと思います。
それと同じような計算を今回はしています。



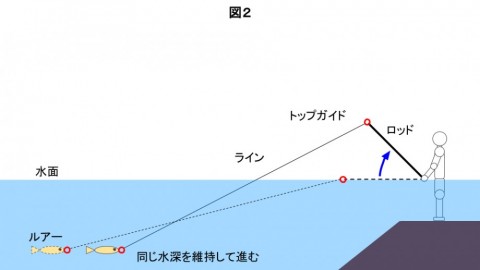
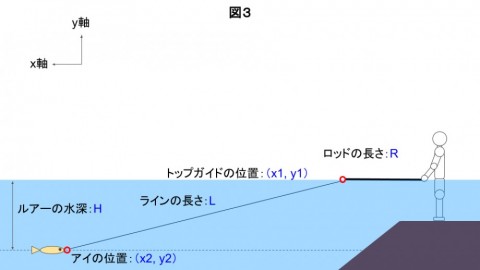
図3は、ロッドを9時の方向にした状態のルアー位置を計算するためのものです。
計算するために、いくつかの変数を定義しておきます。
ロッドの長さ：R
トップガイドの位置（横方向）：x1
トップガイドの位置（縦方向）：y1
ラインの長さ（≒ キャスト距離）：L
ルアーの水深：H
ルアーのアイの位置（横方向）：x2
ルアーのアイの位置（縦方向）：y2



それでは、計算の説明をしていきます。
まず初めに、計算における原点を定めます。
今回は、手の位置を原点とし、座標（0, 0）とします。
手の位置から、横方向（x方向）と縦方向（y方向）にどれだけの距離があるのかを計算していきます。

トップガイドの位置は簡単です。
横方向の位置は、ロッドの長さと等しくなります。
x1 = R
縦方向の位置は、手と同じ位置なので、0になります。
y1 = 0

次に、ルアーのアイの位置について考えていきます。
縦方向の位置は、水深Hと等しくなります。
y2 = -H（原点よりも下なので、マイナスをつけています）
横方向の位置は、少し難しいので図4を見てください。



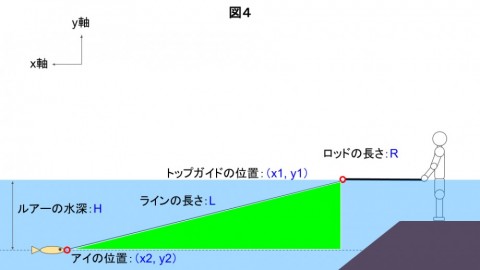
図4には、緑の直角三角形を描きました。
直角三角形の斜辺 = ラインの長さLになっています。
直角三角形の高さ = 水深Hになっています。
直角三角形の底辺 = トップガイドからルアーのアイまでの距離になっています。
ここで、中学生の頃に習った三平方の定理（ピタゴラスの）を思い出してください。
直角三角形においては、「斜辺の2乗 = 高さの2乗 + 底辺のの2乗」となります。
すなわち、底辺＝√（斜辺の2乗 - 高さの2乗）となります。
求めた底辺にトップガイドの位置を足すことで、ルアーのアイの位置が出ます。
x2 = √(L^2 - H^2) + x1
「^2」は「2乗」という意味です。
今回は、ルアーの水深は維持することを前提としています。
したがって、横方向のルアーのアイの位置x2が、ジャークすることでどう変化するのかがポイントになります。

それでは、ジャーク時のトップガイドの位置とルアーのアイの位置を求めていきます。
もう計算の話は勘弁してくれという方も多いと思うので、詳細は割愛させていただきます。
高校数学の三角関数（sin, cos, tan）が出てきますが、よくわからないという方は後述する数値例をご覧ください。
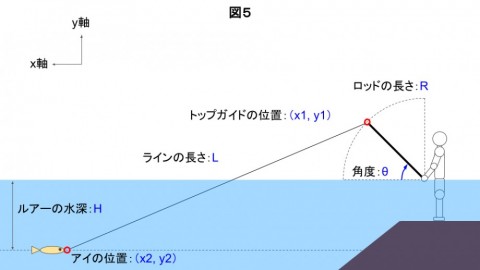
図5は、角度θだけロッドを立てたときの各種変数を示しています。
トップガイドの位置はsinとcosで表現することになりますが、それ以外は直角三角形と三平方の定理で考えることができるので、興味のある方は計算してみてください。

x1 = R × cosθ
y1 = R × sinθ
x2 = √(L^2 - (H+y1)^2) + x1
y2 = -H



以上で計算式は出せました。
あとは、計算式に具体的な数値を当てはめていくだけです。
とは言うものの、変数が多すぎて何をどう見ていくべきかが難しいですよね。
いくつかの項目に分けて、具体的な数値の計算と考察をしていきたいと思います。

●ジャーク角度を変えてみた
下記仮定のもと、ジャーク角度に対応するルアー位置を計算しました。
なお、ルアー位置は横方向のx2だけを示します。
ロッドの長さ：9 feet
ラインの長さ（≒ キャスト距離）：70 m
ルアーの水深：3 m

ジャーク角度 vs ルアー位置
0°のとき：72.68 m
30°のとき：72.24 m
60°のとき：71.16 m
90°のとき：69.76 m

当たり前ですが、ロッドを立てるほどルアーは手前に来ることがわかります。
次に、ロッドの角度を30°ずつ変えたときに、ルアーがどれだけ移動しているのかを、上記数値の差分から見てみました。
0° → 30°のとき：0.440 m = 440 mm
30° → 60°のとき：1.074 m = 1,074 mm
60° → 90°のとき：1.401 m = 1,401 mm

面白いですね。
ジャークの角度は同じ30°なのに、どの角度でジャークするのかによって、3倍以上もルアーの移動距離が変わってきます。
本当か？計算ミスじゃないのか？と僕も思いました。
しかし、考えてみれば当たり前のことでした。
あくまでも、「ルアーの水深は維持すること」を前提にしています。
ロッドを9時の方向から10時の方向にしたとき、トップガイドは横方向よりも縦方向に動きますよね？
ロッドを11時の方向から12時の方向にしたとき、トップガイドは縦方向よりも横方向に動きますよね？
つまり、ロッドを立てている方が、角度を変えた際にトップガイドが横方向に移動しやすいということです。
トップガイドが横方向に移動しやすいとは、ルアーを横方向に移動しやすいということです。
ルアーを細かく動かしたいときは、ロッドを寝かせた状態でジャークすべきであり、ルアーを大きく動かしたいときは、ロッドを立たせた状態でジャークすべきであることがわかりました。
ただし、ルアーを大きく動かしたいときは、そもそもジャークする角度を大きくすべきですよね。
なので、基本的にはロッドを寝かせた状態にして、ルアーを動かしたい距離に応じてジャーク角度を変えていくのが正解だと思います。
どうでしょうか？
自分たちが当たり前のようにやっていた行動が、数学的に正しいと証明されると気持ち良くないですか？
僕はとても気持ちいいです。笑

●ロッドの長さを変えてみた
下記仮定のもと、ロッドの長さに対応するルアー移動距離を計算しました。
なお、ルアー移動距離は横方向だけを示します。
ジャーク角度：0° → 30°
ラインの長さ（≒ キャスト距離）：70 m
ルアーの水深：3 m

ロッド長さ vs ルアー移動距離
7 feet：340 mm
8 feet：390 mm
9 feet：440 mm
10 feet：490 mm

この結果も当然ではありますが、ロッドが長い方がルアーの移動距離は大きくなりますね。
とはいえ、思っていたよりも差分はないと感じました。
7 feet と 10 feet では、ロッド長さは0.914 m = 914 mm も異なります。
しかし、ジャーク時のルアー移動距離は160 mmしか変わりません。
これを大きいと感じるか、小さいと感じるか、人それぞれだと思います。
ジギングのような縦の釣りでは、また違った計算結果になると思います。
リップ付きミノーを用いた横の釣りに限れば、ロッド長さによるジャークへの影響はこの程度ということです。
個人的には小さいと感じております。

●ラインの長さ（≒ キャスト距離）を変えてみた
下記仮定のもと、ロッドの長さに対応するルアー移動距離を計算しました。
なお、ルアー移動距離は横方向だけを示します。
ロッドの長さ：9 feet
ジャーク角度：0° → 30°
ルアーの水深：3 m

ライン長さ vs ルアー移動距離
70 m：440 mm
50 m：469 mm
30 m：537 mm
10 m：913 mm

どうでしょうか？
僕はこの数字を見て、とても驚きました。
一定のスピードでリールを巻きながら、同じ角度でジャークしているのに、ルアーの動きはどんどん大きくなっているということです。
ライン長さが短くなるほど、ルアーの動きが大きくなるというのは、計算結果としては確かだと思います。
ただし、数値自体はその通りではないと考えてください。
あくまでも、ルアーが同じ水深を維持すること前提に計算しています。
しかし、ルアーが手前に来るほど、ルアーが引っ張られる角度が大きくなります。
すなわち、ルアーを上方向に引っ張る力がどんどん大きくなっていきます。
なので、いくらリップ付きのミノーだとしても、現実的には同じ水深を維持することはできません。
皆様も、ミノーを回収するときに、手前に来るほど水面に近づいてくる愛くるしい姿をいつも見ていると思います。
したがって、上記計算結果の数値を鵜呑みにしないでください。
10mの位置にいるからといって、30°のジャークで913 mmもルアーが動くとは考えないでください。
とは言え、ラインが短いほどルアーの動きが大きくなるのは事実だと思います。
「ルアーを回収していたら手前で食ってきた！」というときは、実はルアーアクションが大きくなっているのがきっかけかも？
皆様がご自分の釣りを深堀りする際のご参考になれば幸いです。

●総括
ロッドを寝かせた状態でジャークした方が、ルアーの移動距離は抑えられる。
ロッドを長くしても、ジャークによるルアーの移動距離は大きく変わらない。
ラインの長さ（≒ キャスト距離）が短いほど、ジャークによるルアーの移動距離は大きくなる。
 

---

■最後に
今回は、ジャークについて考えてみました。
やはり、計算に落とし込んで定量的な比較をすることで、新しい気づきがあるものだと思いました。
あくまで素人が計算したものであり、絶対に正しいとは考えていません。
ただし、「相対的な傾向」は信じてもいいのかなと思いました。
また、今回はロッドを寝かせた状態でジャークすることは、より細かくルアーを操作する観点で合理的なのだと理解できたのがよかったです。
そもそもラインが風の影響を受けないようにと、ロッドは寝かせるように意識していました。
ただ、ジャークの観点でも、メリットがあるとわかってよかったです。

現在は深夜1時30分を過ぎています。
図を描いたり数式を考えたり、具体的な数字で示すときに何がわかりやすいかなどを考えたり、やることが多くて1週間で終わらせることができるかどうか心配でした。
一応記事にできるレベルにはなりましたが、まだまだ考えたいことがたくさんあります。
堤防や自磯など、水面から高さがある場合はどうなるのか？
糸ふけの回収はどのくらいかかるのか？
糸ふけの回収も加味したとき、ルアーはどう動くのか？
ロッドの硬さは考慮できるのか？
などなど。
あと2回くらいは、ジャークの深堀りになってしまいそうです。
今回の記事も含めて、少しでも皆様のお力になれていれば幸いです。

最後まで読んでいただきありがとうございました。
次回も引き続き、ジャークについて深堀りしてみたいと思います。
よろしくお願いいたします。