【波止の上にも３年】沖堤三角理論（５）

前回までをご覧になっていない方は下記もご参考ください。

沖堤三角理論（１）：
http://www.fimosw.com/u/menthol/1fa8fdcdsvtjxy
沖堤三角理論（２）：
http://www.fimosw.com/u/menthol/1fa8fdcjt7gjsi
沖堤三角理論（３）：
http://www.fimosw.com/u/menthol/1fa8fdc2385asi
沖堤三角理論（４）：
http://www.fimosw.com/u/menthol/1fa8fdcgaznbzw

テクトロ編（後編）

前編では、テクトロするときの水の中のイメージを計算によって導き出すことで徐々に鮮明に見えてきたのではないかと思う。

このテクトロ編にも“実戦に役立つ法則”が存在するため、後編はその法則を使って更に実戦に落とし込んでいきたいと思う。

前編と同じく高さh＝10mの堤防を例に説明する。

図１：

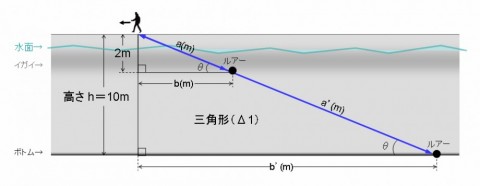
まず、ラインの長さを図るにはどうするのかというと、自分の「足」を使う。

正確に言うと、三角形Δ1（デルタ1）の底辺bまたはb'を足を使って作ることで、ラインの長さを確定し、必要な歩行速度を求める。

まずは測定し易いように50cmの歩幅で歩くルールを決める。

そして以下の基本的な手順で、

1.ルアーを水面に置く
2.ラインをフリーにして歩く
3.ラインを張る（Δ1ができる）

これだけで理想的な三角形Δ1が出来ているはず。そして、

4.テクトロを開始する

基本動作としてはこれだけだ。

ミノーはフォールスピードが遅く、スピンテールやバイブレーションなどはミノーの倍または倍以上のスピードで落ちていく。

だから歩き終えた時点でルアーは丁度よいレンジまで沈んでいるため、そのまま手際よく繋いでいくことができるはずだ。

θ＝30℃のとき、

上層狙いの場合の底辺bは、前編で必要数とした10mを基準にすると１歩50cmの歩幅で20歩。

ボトム狙いの場合は、b'＝10(ｍ)%*√3＝17.32(m)≒35歩となる。

Δ1の底辺を作る作業として、この必要な歩数を歩けばいいという考え方なら日の出前の暗闇でも難なく展開していけるはずだ。

ミノーは水を噛ませて沈める性質のルアー（ルアーのスペックにより潜行深度が決まる）なので、十分なラインの長さが足りていれば、後は魚に喰わせやすい歩行速度で歩くだけ。

とはいえ、ミノーであっても“ラインの長さを超えるレンジにミノーは到達しない”ことは頭に入れておく必要はある。

更に実戦に落とし込んでいく。

やや面倒なのがボトム狙いのときで、大体にして35歩などという歩数が実に中途半端だ。

しかし１オンスまたはそれ以上の重量級ルアーでボトムを狙うとき、実は三角形Δ1の底辺b'は任意の歩数で対応することができる。

そもそも実戦では都合良く角度θ＝30℃にはならないはずだ。

実戦での考え方として必要なことは、θの角度が何度なのかということではなく“最初に作るΔ1の形をテクトロ開始後も維持すること”である。

テクトロ開始後のθの維持とは、＝レンジをキープすることであり、また必要な歩行速度を求めることに繋がる。

例えば、Δ1の底辺b'＝30歩として計算してみる。

ルアーのフォール速度Fx＝1（m/s）とした場合のベクトル計算（下、図２）の三角形Δ2の各辺の比率はΔ1の1/10（h/Fx）ということになる。

従って、レンジキープするための歩行速度F＝30(歩)/10＝3歩（m/s）となる。

図２：

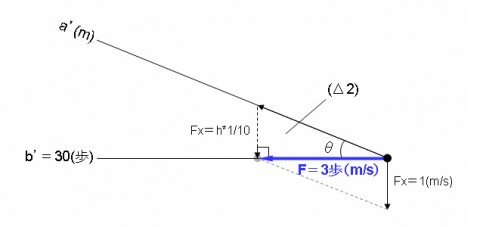
以上の計算結果から下記の法則を導き出すことができる。

歩行速度F（m/s）＝ b'*（Fx/h）

つまりh＝10mの堤防のΔ2の歩行速度Fは、アングラーが任意に決定するb'により以下のように推移することが分かる。

- Δ1のb'＝１０歩のとき、歩行速度F＝1歩(m/s)
- Δ1のb'＝２０歩のとき、歩行速度F＝2歩(m/s)
- Δ1のb'＝３０歩のとき、歩行速度F＝3歩(m/s)
- Δ1のb'＝４０歩のとき、歩行速度F＝4歩(m/s)
・
・
・

以上の結果をフォール速度Fx＝0.5(m/s)のルアーに当てはめて計算するとこうなる。

- Δ1のb'＝１０歩のとき、歩行速度F＝0.5歩(m/s)
- Δ1のb'＝２０歩のとき、歩行速度F＝1歩(m/s)
- Δ1のb'＝３０歩のとき、歩行速度F＝1.5歩(m/s)
- Δ1のb'＝４０歩のとき、歩行速度F＝2歩(m/s)
・
・
・

最初に書いた手順を纏めると下記の通り。

1.ルアーを水面に置く
2.ラインをフリーにしたまま歩く
　　- 上層：20歩
　　- ボトム：b'歩（b'は任意）
3.ラインを張る
4.テクトロを開始する
　　- 上層：任意の歩行速度
　　- ボトム：２で決めたb'及びフォール速度Fxにより決定
　　　　＜フォール速度Fx＝1(m/s)のとき＞
　　　　- b'＝10歩のとき、歩行速度F＝1歩(m/s)
　　　　- b'＝20歩のとき、歩行速度F＝2歩(m/s)
　　　　- b'＝30歩のとき、歩行速度F＝3歩(m/s)
　　　　- b'＝40歩のとき、歩行速度F＝4歩(m/s)
　　　　＜フォール速度Fx＝0.5(m/s)のとき＞
　　　　- b'＝10歩のとき、歩行速度F＝0.5歩(m/s)
　　　　- b'＝20歩のとき、歩行速度F＝1歩(m/s)
　　　　- b'＝30歩のとき、歩行速度F＝1.5歩(m/s)
　　　　- b'＝40歩のとき、歩行速度F＝2歩(m/s)

とはいえ、b'があまり短いと立ち回りがしんどいのでボトムを叩くときはb'＝20～30歩程度で理想的なΔ1を作るのがやりやすい。

この計算に慣れてくると、他のアングラーの立ち回りを見れば大凡どのレンジをどのように攻めているかが何となく見えてくるようになる。

他のアングラーの後方を行く場合は叩かれてないレンジから引けばよいし、逆に他の人が当たっていれば同じレンジに合わせればよい。

また、ボトムに反応が出ないから歩きながら中層に切り替えたいなどというときに「可変歩行」にも対応することができる。

答えは簡単、ボトムを引いている時に中層へ切り替えるには“２倍の歩行速度”に切り替えればよい。

例えば、b'＝30歩、F＝3歩（m/s）でボトムを引いてから中層へ切り替える場合は図３の通りである。

図３：

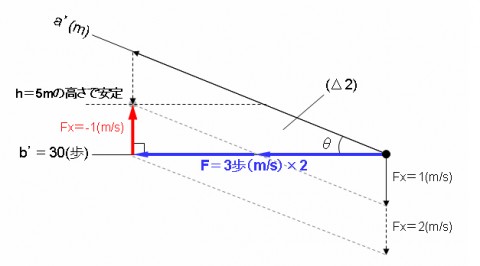
テクトロ開始後にF＝3歩から6歩（1mの歩幅で3歩）へと、立ち回りを変更した場合、

6歩（3m）はb'の1/5であることから、Δ2のFx＝2m（m/s）

ただ、実際のFxは1（m/s）の固定値になるため上方向へのベクトル-1（m/s）が作用し、ルアーは徐々に上昇することになる。

そして、h＝5mの高さに到達するとルアーの上昇は止まり安定。

h＝5mのレンジをキープしながらルアーを通すことになる。

特に釣れてないときなどは、もう少し上、もう少し下、といったように細かいレンジを探りたくなるが、もう一つのレンジ補正の方法としてラインの長さを変える方法がある。

θ＝30℃に近い理想的なΔ1を最初に作ってあれば、1:2√3の辺の比率から、

- レンジを1m上げる＝ラインを2m巻く
- レンジを2m下げる＝ラインを4m出す

ということだ。

このような感じでレンジの微調整ができる。

ついでに説明すると、ここでリールのレバーブレーキ（LB）が大活躍する。

特にラインを出すときはハンドルの逆回転を見れば、人差し指パチンだけで後は見た目の判断ができるからだ。

私がLBブランジをいつまでも手放さないのは実はこれが理由。

所謂ハイギア、１回転あたりの巻き取り量が1mに近いスペックがこの釣りにマッチしているしね。

ただ、選択肢がまだ少ないのでハイエンド以外のクラスでもラインナップを増やしてほしいなあと思う。（＞ダイワさん）

嫌いな釣りと言いながら大分長くなってしまったテクトロ編は以上だ。

ディープエリアの真相は水の中。

地上から見えないからわからない。

それを利用してというか、“最初に言ったもの勝ち”みたいな雰囲気を察することがあるが、そのノリ（？）はどうもね…。

こういった計算による“裏付け”が大事だと思う。